Python SciPy Tutorial - Una guida per principianti

Introduzione

L'informatica è una parte essenziale della ricerca scientifica. I problemi matematici, ingegneristici, scientifici e altri tecnici sono complessi e richiedono potenza e velocità di calcolo. Python fornisce la libreria SciPy per la risoluzione di problemi tecnici in modo computazionale.

Questo articolo presenta un tutorial SciPy e come implementare il codice in Python con esempi.

Prerequisiti

• Installato Python 2.7 o Python 3
• Un ambiente Python per l'esecuzione del codice.
• Libreria SciPy installata.
• Libreria NumPy installata (segui la nostra guida:Come installare NumPy).
• Libreria Matplotlib installata per la stampa (opzionale).

Cos'è SciPy?

SciPy (Sci interessante Py thon) è un modulo di calcolo scientifico open source per Python. Basato su NumPy, SciPy include strumenti per risolvere problemi scientifici. Gli scienziati hanno creato questa libreria per soddisfare le loro crescenti esigenze di risoluzione di problemi complessi.

SciPy vs NumPy

La libreria NumPy (Num erica Py thon) esegue calcoli numerici. Gli scienziati utilizzano questa libreria per lavorare con gli array poiché NumPy copre usi elementari nella scienza dei dati, nella statistica e nella matematica.

SciPy copre calcoli e funzioni avanzati. Questa libreria aggiunge più funzionalità di data science, tutte le funzioni di algebra lineare e algoritmi scientifici standard.

Perché usare SciPy?

La libreria SciPy si basa su NumPy e opera su array. La potenza di calcolo è veloce perché NumPy usa C per la valutazione.

Lo stack scientifico di Python è simile a MATLAB, Octave, Scilab e Fortran. La differenza principale è che Python è facile da imparare e da scrivere.

Sottopacchetti SciPy

La libreria SciPy ha diversi gruppi di sottopacchetti. Ci sono due modi per importare sottopacchetti dal modulo SciPy:

import scipy.<sub package name> as <alias>

O in alternativa:

from scipy import <sub package name> as <alias>

In entrambi i metodi di importazione, l'alias è facoltativo.

Funzioni SciPy

SciPy include molte delle funzioni di array primarie disponibili in NumPy e alcuni dei moduli comunemente usati dai sottopacchetti SciPy.

Per importare una funzione da un sottopacchetto, utilizzare:

from scipy.<subpackage> import <function>

Funzioni di base

Per ottenere aiuto e informazioni per qualsiasi funzione SciPy, usa il help() comando:

help(<name of function>)

Il help() il comando non ha bisogno di parametri. Dopo l'esecuzione senza parametri, viene visualizzato un prompt in cui si inserisce il nome della funzione.

Un altro modo rapido per ottenere aiuto con qualsiasi comando in Python è scrivere il nome del comando, mettere un punto interrogativo alla fine ed eseguire il codice.

Funzioni speciali

Le funzioni speciali nel modulo SciPy includono calcoli e algoritmi comunemente usati. Tutte le funzioni speciali accettano gli array NumPy come input. I calcoli sono elementi.

Per importare lo special sottopacchetto, usa:

import scipy.special as special

O in alternativa:

from scipy import special

Per importare una funzione specifica dallo special sottopacchetto, usa:

from scipy.special import <function name>

Fattoriale

Valuta il fattoriale di qualsiasi numero eseguendo:

special.factorial(<integer or array>)

Ad esempio, per trovare il fattoriale di dieci, usa:

special.factorial(10)

Permutazioni e combinazioni

Per trovare il numero di permutazioni, usa:

special.perm(<number of elements>, <number of elements taken>)

Ad esempio, per vedere il numero di permutazioni di tre elementi presi due alla volta:

special.perm(6,2)

Allo stesso modo, trova il numero di combinazioni con:

special.comb(<number of elements>, <number of elements taken>, repetition=<True or False>)

Per trovare il numero di combinazioni di tre elementi presi due alla volta con ripetizione, inserisci:

special.comb(6,2, repetition=True)

Permutazioni e combinazioni sono utilizzate negli algoritmi di ordinamento informatici.

Funzioni esponenziali

Le funzioni esponenziali valutano gli esponenti per basi diverse.

Calcola gli esponenti di base dieci con:

special.exp10(<integer or array>)

Ad esempio:

special.exp10([0,1,2])

L'informatica usa spesso funzioni esponenziali di base due:

special.exp2(<integer or array>)

Calcola la decima potenza di base due con:

special.exp2(10)

Somma logaritmica degli esponenziali

La somma logaritmica degli esponenziali (LSE o LogSumExp) è un'approssimazione utilizzata dagli algoritmi di apprendimento automatico. Calcola l'LSE con:

special.logsumexp(<integer or array>)

Funzione di Bessel

Le funzioni di Bessel compaiono nella propagazione delle onde, nell'elaborazione del segnale e nei problemi di potenziale statico. Trova la funzione di Bessel del primo tipo con:

special.jn(<integer order>, <integer or array>)

Approfitta dell'intero stack per visualizzare la funzione di Bessel. Per trovare la funzione di Bessel del secondo ordine del primo tipo, utilizzare:

#import stack
import scipy.special as special
import matplotlib.pyplot as plt
import numpy as np
#The X-axis
x = np.linspace(1,50,100)
#Bessel function of the first kind order two
jn1 = special.jn(2,x)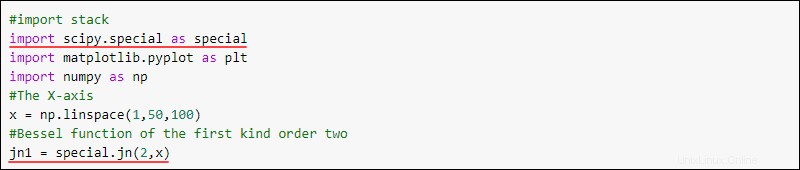

Traccia i risultati:

#Plotting
plt.title('Bessel function first kind order two')
plt.plot(x, jn1)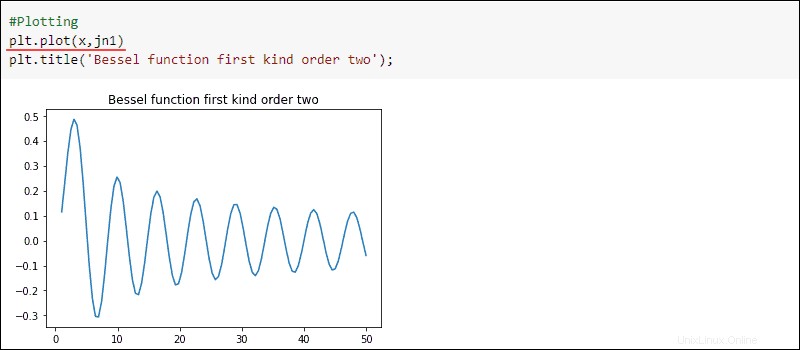

Integrazione e funzioni ODE

SciPy fornisce un sottopacchetto per i calcoli con integrali definiti. Per importare l'integrate sottopacchetto, usa:

import scipy.integrate as integrate

O in alternativa:

from scipy import integrate

Importa una funzione specifica dal sottopacchetto integrate con:

from scipy.integrate import <function name>

Integrazione generale

Calcola una singola variabile integrale con il quad funzione da integrate sottopacchetto:

integrate.quad(<function>, <lower limit>, <upper limit>)

La function l'input è definito utilizzando una funzione lambda.

Ad esempio, per calcolare l'integrale definito della funzione x+1 tra zero e uno:

from scipy import integrate
f = lambda x: x+1
integrate.quad(f, 0, 1)

L'output mostra due valori. Il primo valore è l'integrale valutato e il secondo è l'errore di stima.

Funzioni di ottimizzazione

SciPy ha un sottopacchetto di ottimizzazione per trovare il minimo o il massimo di una funzione. L'optimize il sottopacchetto include solutori e algoritmi per trovare valori ottimali locali e globali.

Per importare il sottopacchetto di ottimizzazione:

from scipy import optimize

Oppure usa:

import scipy.optimize as optimize

Per importare una funzione specifica dal sottopacchetto optimize , esegui:

from scipy.optimize import <function name>

Riduci a icona una funzione

Trovare un minimo di una funzione viene utilizzato nell'apprendimento automatico per ridurre la perdita (o l'errore) di un algoritmo.

Ad esempio, puoi creare una funzione e trovare il minimo. Per farlo, usa il fmin funzione da optimize sottopacchetto in SciPy:

#Import stack
import numpy as np
from scipy import optimize
#Defining inverse sine function
def f(x):
    return -np.sin(x)
#X-axis
x = np.linspace(0,5,100)
#Starting point
start = 3
#Simplex algorithm for optimization
optimized = optimize.fmin(f,start)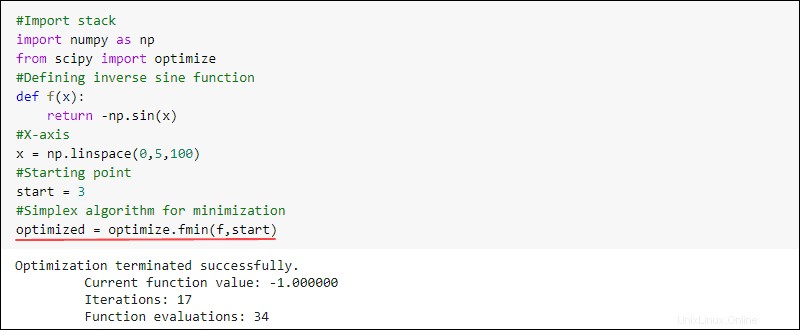

Per tracciare il risultato, esegui:

import matplotlib.pyplot as plt
plt.plot(x, f(x))
plt.scatter(start,f(start))
plt.scatter(optimized, f(optimized))
plt.legend(['Function -sin(x)', 'Starting point', 'Optimized minimum'])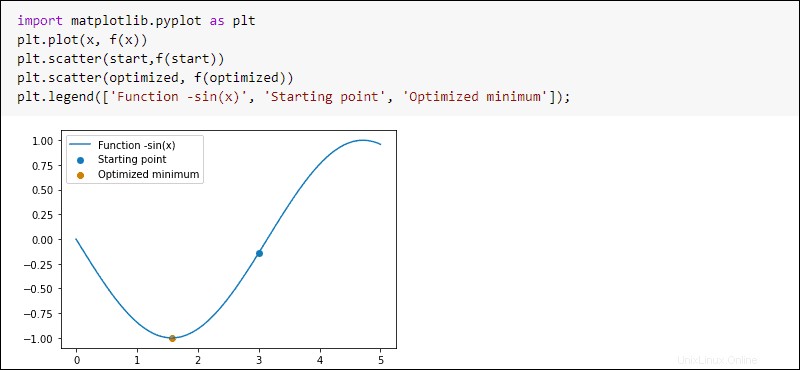

Funzioni di trasformazione di Fourier

SciPy include un sottopacchetto per le funzioni di trasformazione di Fourier chiamato fftpack . Le trasformazioni sono trasformazioni discrete di Fourier (DFT). Tutte le trasformazioni vengono applicate utilizzando l'algoritmo Fast Fourier Transformation (FFT).

Per importare il fftpack sottopacchetto, usa:

import scipy.fftpack as fftpack

Oppure:

from scipy import fftpack

Trasformazione veloce di Fourier

Ad esempio, crea una funzione periodica come somma di tre onde sinusoidali:

import numpy as np
freq_samp = 100
#Time
t = np.linspace(0, 1, freq_samp*2, endpoint = False )
#Frequencies
f1, f2, f3 = 1, 5, 20
#Amplitudes
A1, A2, A3 = 3, 2, 1
x1 = A1*np.sin(f1*2*np.pi*t)
x2 = A2*np.sin(f2*2*np.pi*t)
x3 = A3*np.sin(f3*2*np.pi*t)
#Sum of waves
x = x1+x2+x3

Traccia le onde usando matplotlib :

import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(t,x1,t,x2,t,x3)
plt.subplot(2,1,2)
plt.plot(t,x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');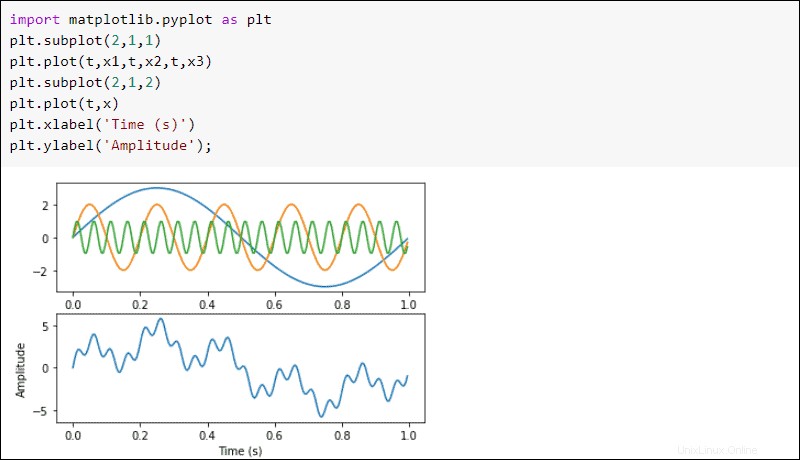

Quindi, applica il fft e fftfreq funzioni dal fftpack per fare una trasformata di Fourier del segnale.

from scipy import fftpack
A = fftpack.fft(x)
freq = fftpack.fftfreq(len(x))*freq_samp*2

Traccia i risultati per vedere il dominio della frequenza:

plt.stem(freq,np.abs(A)/freq_samp,use_line_collection=True)
plt.xlim(-25,25)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()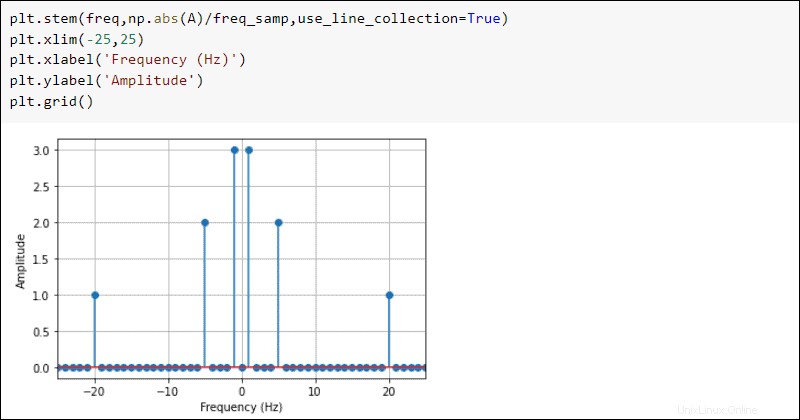

Funzioni di elaborazione del segnale

Il sottopacchetto signal include funzioni utilizzate nell'elaborazione del segnale. Per importare signal , esegui:

import scipy.signal as signal

O in alternativa:

from scipy import signal

Convoluzione

Un compito comune nell'elaborazione del segnale è la convoluzione. Il sottopacchetto SciPy signal ha la funzione convolve per svolgere questo compito. Ad esempio, crea due segnali con frequenze diverse:

import numpy as np
#Time
t = np.linspace(0,1,100)
#Frequency
f1, f2 = 5, 2
#Two signals of different frequencies
first_signal = np.sin(f1*2*np.pi*t)
second_signal = np.sin(f2*2*np.pi*t)

Traccia i segnali:

import matplotlib.pyplot as plt
#Plotting both signals
plt.subplot(2,1,1)
plt.plot(t, first_signal)
plt.subplot(2,1,2)
plt.plot(t, second_signal)
plt.ylabel('Amplitude')
plt.xlabel('Time (s)')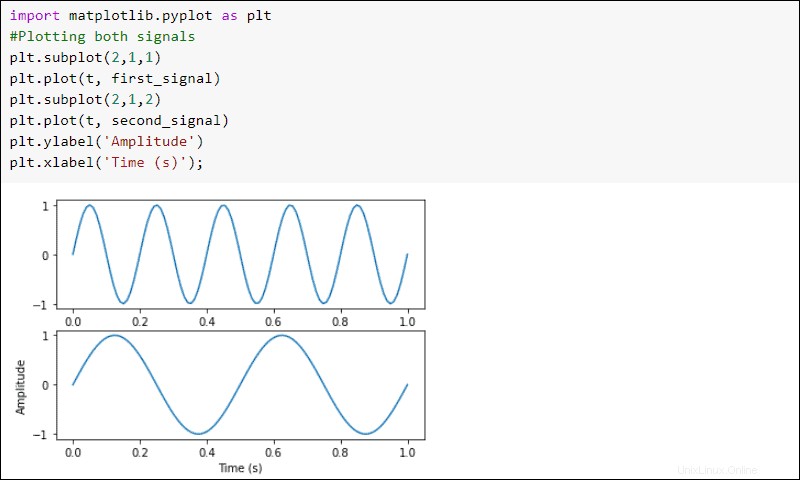

Importa il signal sottopacchetto da scipy . Usa il convolve funzione dal signal sottopacchetto per far confluire i due segnali:

#Importing the signal subpackage
from scipy import signal
#Convolving two signals
convolution = signal.convolve(first_signal, second_signal, mode='same')

Traccia i risultati:

#Plotting the result
plt.plot(t, convolution)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')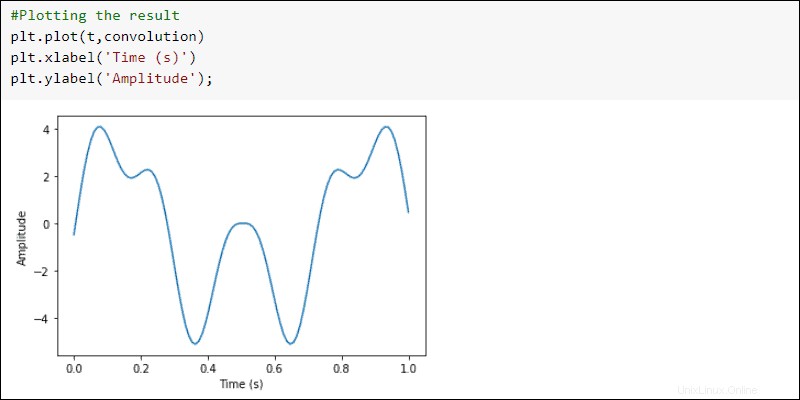

Funzioni di interpolazione

L'interpolazione viene utilizzata nel campo dell'analisi numerica per generalizzare i valori tra due punti. SciPy ha l'interpolate sottopacchetto con funzioni di interpolazione e algoritmi.

Importa l'interpolate sottopacchetto con:

import scipy.interpolate as interpolate

Oppure:

from scipy import interpolate

Interpolazione unidimensionale

Lo SciPy interpolate il sottopacchetto ha il interp1d funzione per l'interpolazione unidimensionale dei dati. Ad esempio, crea un giocattolo dati utilizzando numpy :

import numpy as np
#Create toy data
x = np.arange(0,10,0.5)
y = np.sin(x)

Interpola i dati con interp1d da interpolate sottopacchetto:

from scipy import interpolate
#Interpolate
f = interpolate.interp1d(x, y)
#Create interpolation function
x_i = np.arange(0,10,3)
y_i = f(x_i)

Traccia i risultati:

#Plot results
plt.scatter(x,y)
plt.plot(x_i, y_i)
plt.legend(['Interpolation', 'Data points'])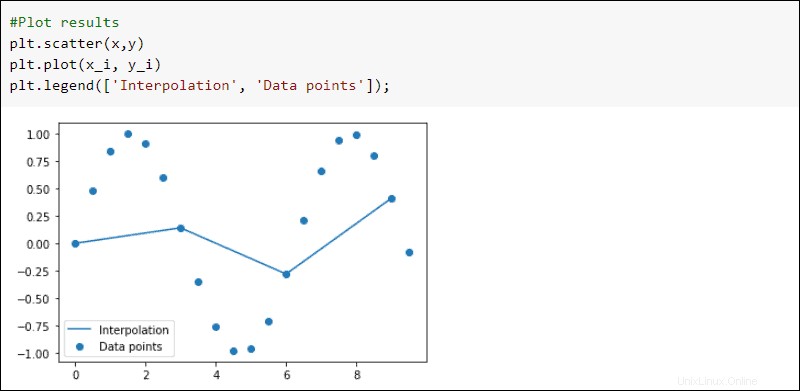

Algebra lineare

SciPy ha un sottopacchetto di algebra lineare completo. Il sottopacchetto SciPy linear algebra è ottimizzato con le librerie ATLAS LAPACK e BLAS per un calcolo più veloce.

Per importare il pacchetto di algebra lineare da SciPy, esegui:

import scipy.linalg as linalg

Oppure usa:

from scipy import linalg

Tutte le funzioni di algebra lineare si aspettano un array NumPy per l'input.

Determinante

Calcola il determinante di una matrice con det dal linalg sottopacchetto:

linalg.det(<numpy array>)

Ad esempio:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the determinant
linalg.det(A)

Matrice inversa

Determina la matrice inversa utilizzando inv :

linalg.inv(<numpy array>)

Ad esempio:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3,4]])
from scipy import linalg
#Calculate the inverse matrix
linalg.inv(A)

Autovettori e autovalori

Autovettori e autovalori sono un metodo di scomposizione di matrici. Il problema autovalore-autovettore è un problema di algebra lineare comunemente implementato.

Il eig La funzione trova gli autovalori e gli autovettori di una matrice:

linalg.eig(<numpy array>)

L'output restituisce due array. Il primo contiene autovalori e il secondo ha autovettori per la matrice data. Ad esempio:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the eigenvalues and eigenvectors
linalg.eig(A)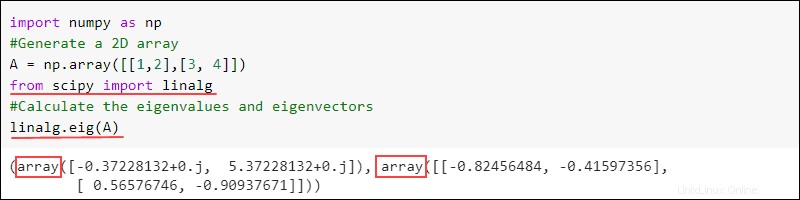

Strutture di dati spaziali e algoritmi

Le strutture dati spaziali sono oggetti costituiti da punti, linee e superfici. SciPy dispone di algoritmi per strutture di dati spaziali poiché si applicano a molte discipline scientifiche.

Importa il spatial sottopacchetto da SciPy con:

import scipy.spatial as spatial

Oppure:

from scipy import spatial

Un notevole esempio di algoritmo spaziale è il diagramma di Voronoi. Per un dato insieme di punti, le mappe di Voronoi dividono un piano in regioni. Se un nuovo punto cade in una regione, il punto nella regione è il vicino più vicino.

Ad esempio, crea un diagramma di Voronoi da venti punti casuali:

from scipy.spatial import Voronoi
import numpy as np
points = np.random.rand(20,2)
voronoi = Voronoi(points)
from scipy.spatial import voronoi_plot_2d
fig = voronoi_plot_2d(voronoi,show_vertices=False)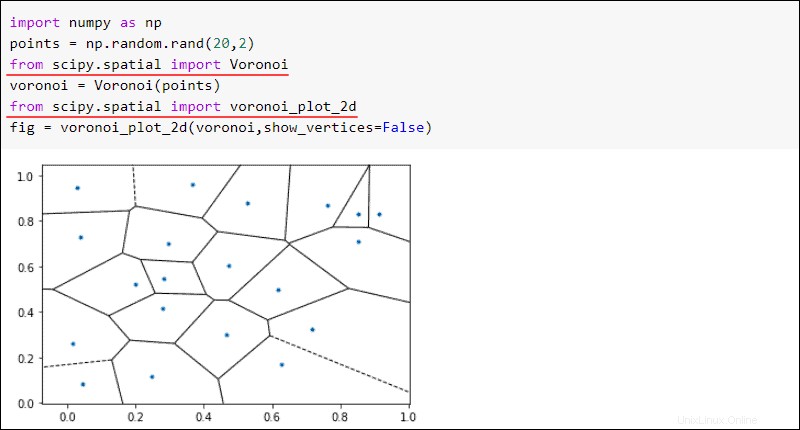

Elaborazione delle immagini

SciPy ha un sottopacchetto per varie elaborazioni di immagini n-dimensionali. Per importare il ndimage sottopacchetto, esegui:

import scipy.ndimage as ndimage

Oppure usa:

from scipy import ndimage

Il misc di SciPy il sottopacchetto contiene un'immagine di esempio a scopo dimostrativo. Per importare le misc sottopacchetto e mostra l'immagine:

from scipy import misc
from matplotlib import pyplot as plt
raccoon = misc.face()
#show image
plt.imshow(raccoon)
plt.show()

Importa il ndimage sottopacchetto e applica un uniform_filter all'immagine. Mostra l'immagine per vedere i risultati:

from scipy import ndimage
filtered = ndimage.uniform_filter(raccoon)
plt.imshow(filtered)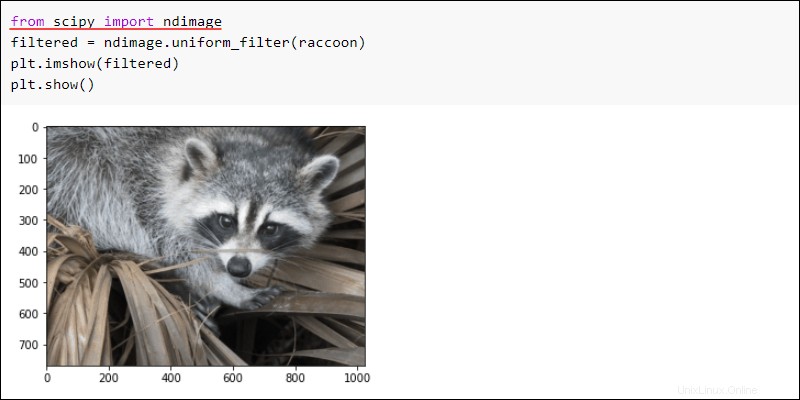

File IO (pacchetto file input/output)

SciPy ha un sottopacchetto di input e output di file chiamato io . Il io il sottopacchetto viene utilizzato per leggere e scrivere formati di dati da diversi programmi e linguaggi di calcolo scientifico, come Fortran, MATLAB, IDL, ecc.

Importa il io sottopacchetto da SciPy con:

import scipy.io as sio

Oppure usa:

from scipy import io as sio