In questo tutorial, discuteremo l'algebra vettoriale e i relativi calcoli in Scientific Linux. Per il nostro scopo, ho scelto Python come linguaggio di programmazione per la sua semplicità e potenza di calcolo. Qualsiasi distribuzione Linux ha per impostazione predefinita un editor/compilatore Python che viene richiamato tramite una finestra del terminale. Esaminiamo alcuni concetti di algebra vettoriale.
Nota:lavoreremo solo sullo spazio reale di due o tre dimensioni.
Algebra vettoriale
L'elemento di uno spazio vettoriale, da un punto di vista matematico, può essere rappresentato come l'array di un numero di elementi che appartengono a quello spazio vettoriale. Più specificamente, e nell'approccio del calcolo numerico, può essere rappresentato come un elenco di numeri reali, che ha tre caratteristiche fondamentali:
Magnitudo
La dimensione del vettore ed è rappresentata con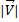 
;questa è la parte scalare di un vettore. Per calcolare la grandezza di un vettore dobbiamo eseguire la seguente formula:
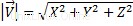
X, Y e Z sono le coordinate vettoriali.
Direzione
La direzione di un vettore è data da una direttrice avente un angolo specifico per ciascun asse del sistema di coordinate chiamato angoli direttrice.
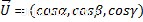
Laddove alfa, beta e gamma sono gli angoli del direttore del vettore ei loro coseni sono i coseni del direttore, possono anche essere calcolati dividendo ciascuna coordinata del vettore per la sua magnitudine.
Orientamento
Uno dei due possibili orientamenti tra la stessa direzione.
Somma algebrica vettoriale
Per fare una somma algebrica di vettori, dobbiamo sommare le coordinate omologhe di due vettori, rispettando le stesse proprietà della somma algebrica di numeri reali. Proprio come segue:
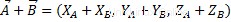Come possiamo vedere, il risultato è un altro vettore, appartenente allo stesso spazio vettoriale.
Prodotto di un vettore da uno scalare
Dati un vettore e uno scalare, il vettore prodotto di uno scalare è definito come il prodotto scalare di ciascuna coordinata del vettore:
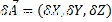
Dove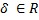 
Unit Vector
Un'applicazione diretta per Product vector da uno scalare è il vettore unitario, a unità vettoriale è un vettore normato di lunghezza 1.
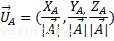
Combinazione lineare
Quando mescoliamo le operazioni passate, somma algebrica e prodotto vettore-scalare, otteniamo una combinazione lineare, in cui il risultato è anche un vettore appartenente allo stesso spazio vettoriale, come è:
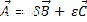
Dove il vettore A è una combinazione lineare di vettori B e C.
Python su Scientific Linux 7.1
Per implementare l'algebra vettoriale abbiamo scelto Python come linguaggio di calcolo. L'editor di testo che scegliamo è gedit e viene fornito per impostazione predefinita con la distribuzione Scientific Linux 7.1.
Magnitudo di un vettore
Chiamiamo gedit utilizzando un terminale o semplicemente fare clic sull'icona nella scheda delle applicazioni:
Per prima cosa dobbiamo lavorare con le liste, in quanto rappresentano vettori e devono essere dichiarate come è:
V=[2, 2, 1]
Dichiariamo una variabile per memorizzare la grandezza e diamo un valore, usiamo 0.
modV=0
Ora usiamo la matematica di classe per operare sulla radice quadrata:
import math
Il calcolo della grandezza:
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
Come possiamo vedere, dobbiamo usare sub-index per indicare l'elemento della lista che opereremo, partendo da 0.
Lo script completo è il seguente:
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
Una volta terminato, dobbiamo salvare il file con estensione .py e individuare il percorso del file e aprire una finestra di terminale con il tasto destro del mouse e quindi "apri nella finestra di terminale". Dopo dobbiamo chiamare l'interprete Python digitando:
$ python [path]/yourfilename.py
questo aprirà una finestra come questa e darà il risultato:
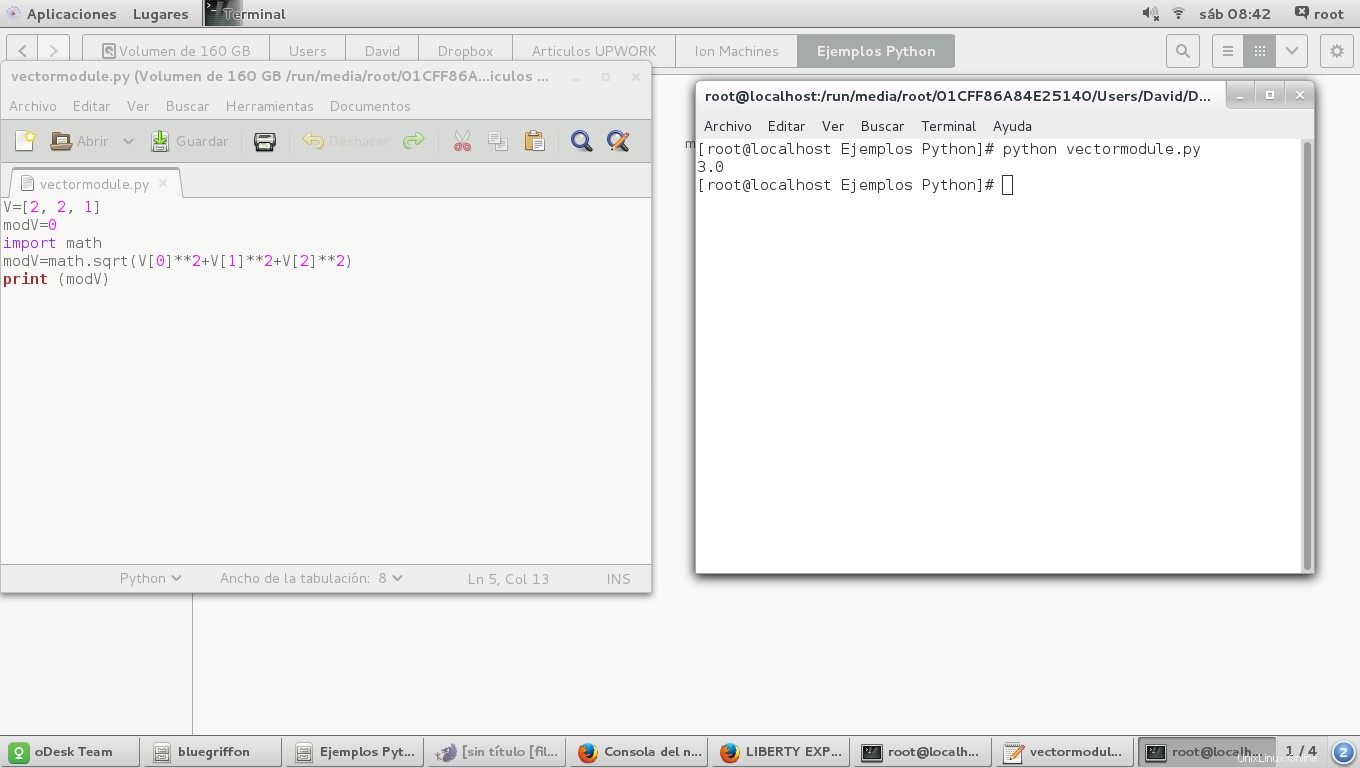
Un altro modo per farlo è usare un ciclo for come questi:
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
Qui dobbiamo usare le tecniche di indentazione poiché l'interprete Python funziona in questo modo.
Direzione di un vettore
Usa la matematica in classe
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
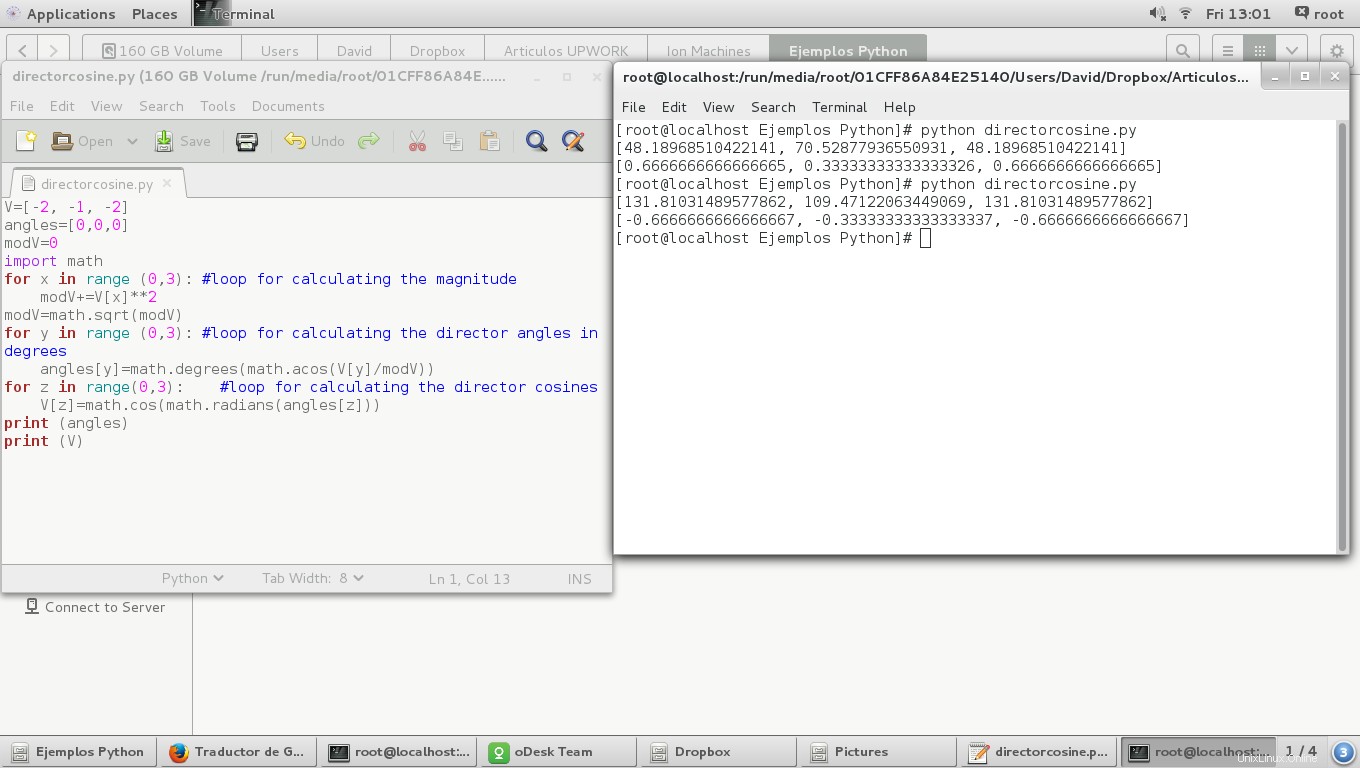
Il risultato è il seguente:
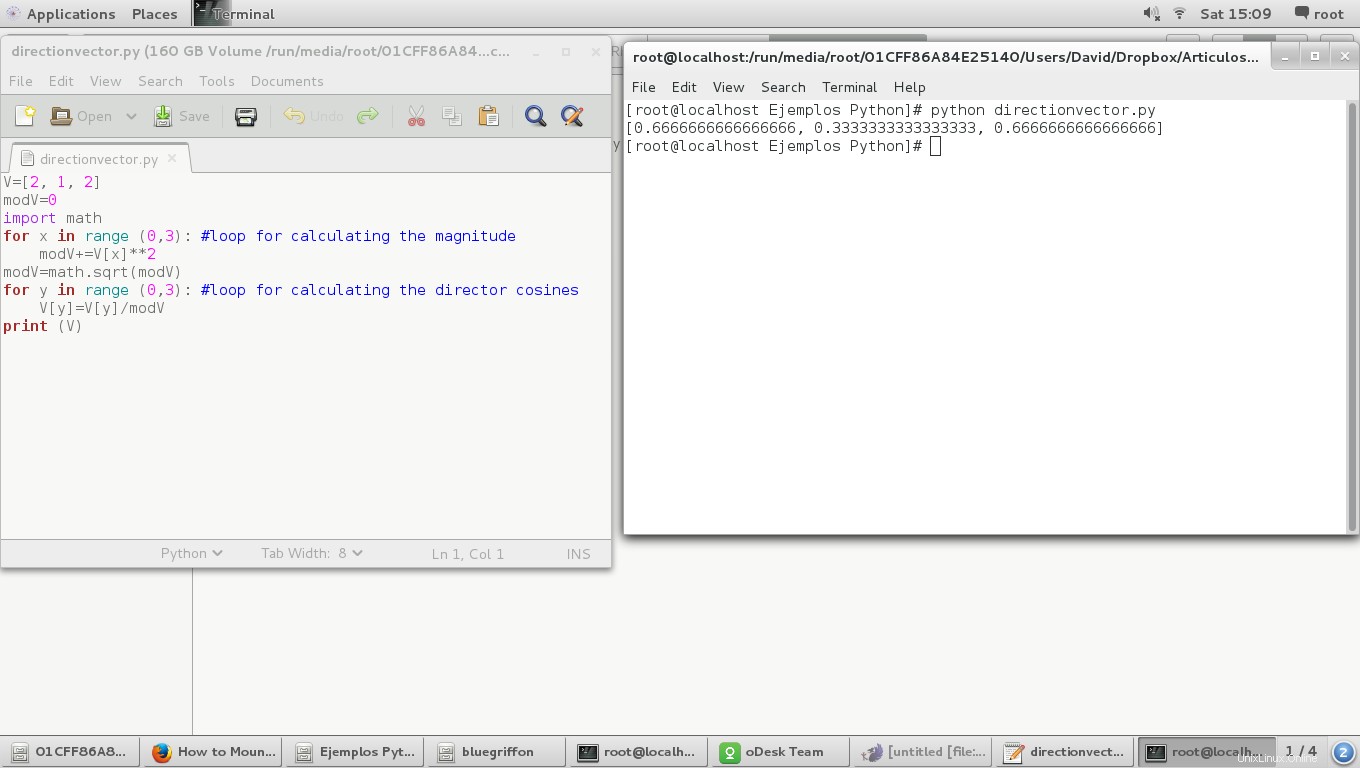
Un altro modo per farlo è usare le funzioni trigonometriche della classe di matematica, semplicemente in questo modo:
Calcoliamo innanzitutto gli angoli della regia:
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
E poi calcoliamo i coseni del direttore e li stampiamo
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
E il risultato:
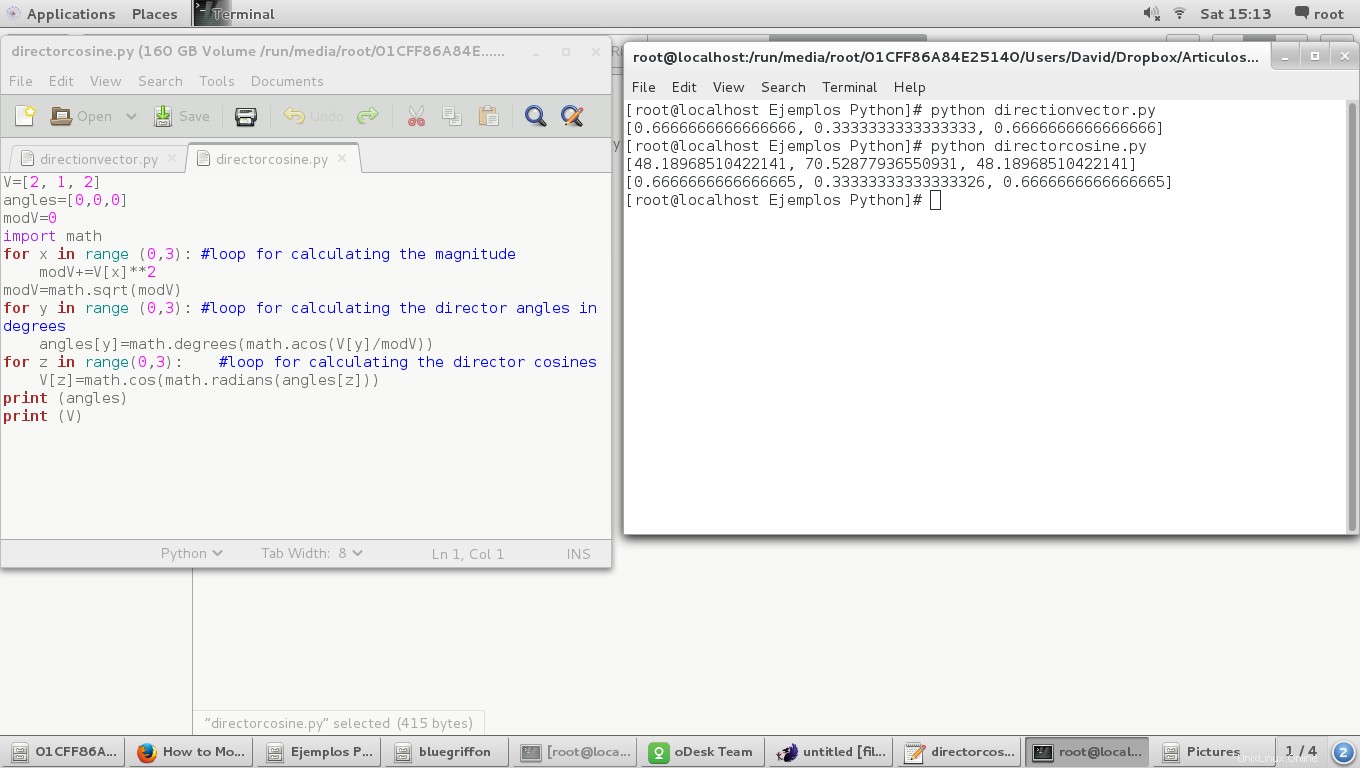
Possiamo osservare che i coseni del direttore hanno lo stesso valore
Orientamento di un vettore
Se cambiamo il segno di tutte le coordinate di un vettore, intrinsecamente, stiamo cambiando l'orientamento del vettore, così com'è:
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
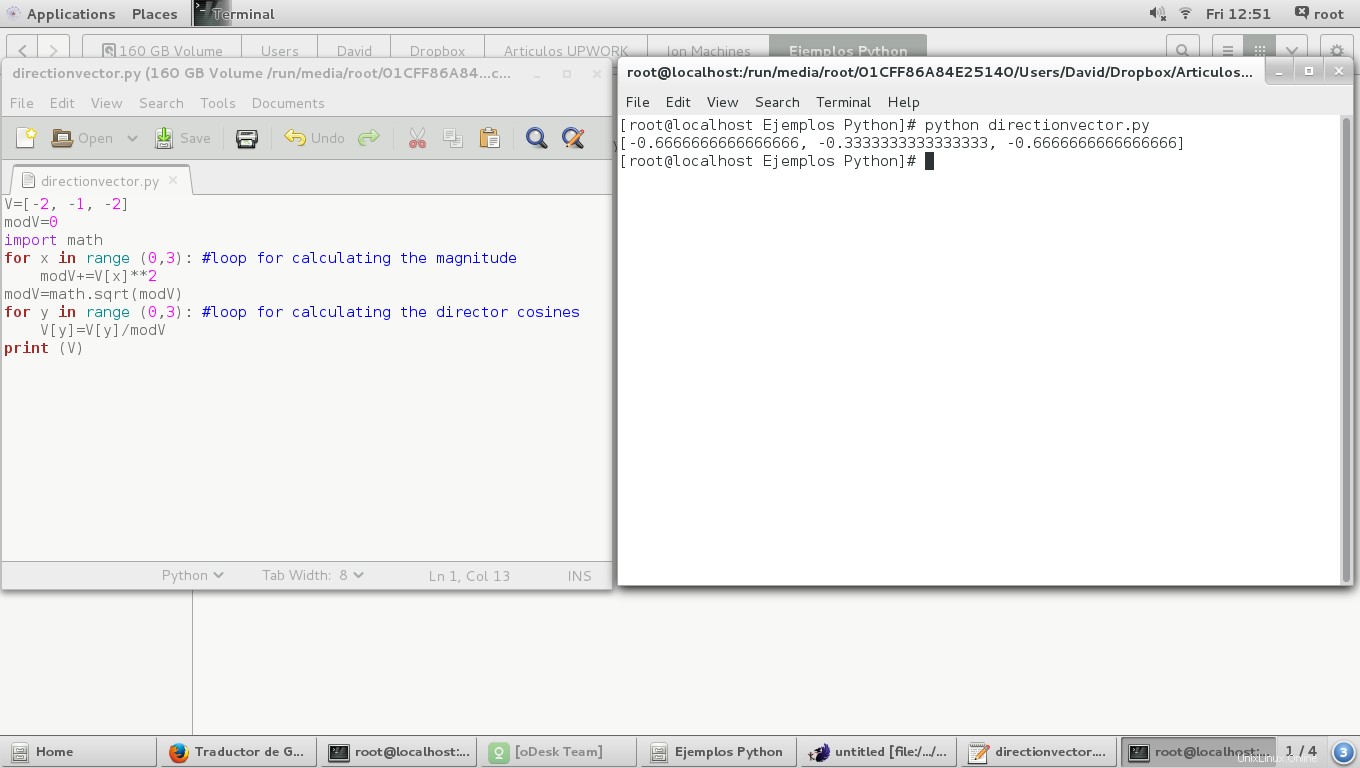
Nell'immagine successiva possiamo vedere gli angoli del regista sono diversi a 180 gradi dagli originali
Somma algebrica vettoriale
Per prima cosa dobbiamo dichiarare tutti i vettori coinvolti nella somma algebrica, così come:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
dove sommiamo A più B e il risultato memorizzeremo in S
L'aggiunta di due vettori (liste) in Python equivale a eseguire un ciclo 'for' per ciascuna coordinata del vettore risultante, quindi dobbiamo fare quanto segue:
for x in range(0,3):
S[x]=A[x]+B[x]
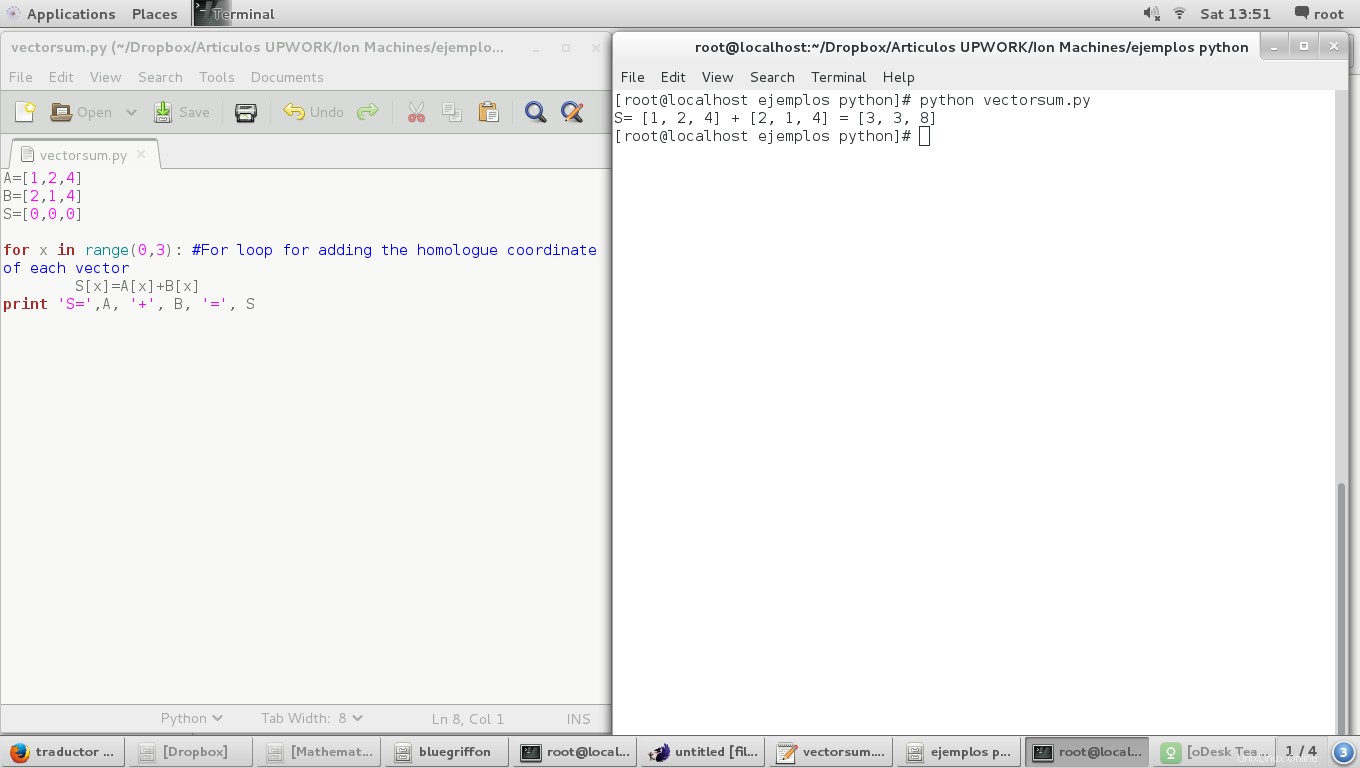
Qui abbiamo lo script completo per la somma vettoriale algebrica:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S
E il risultato è:
Prodotto di un vettore da uno scalare
Dato un vettore:
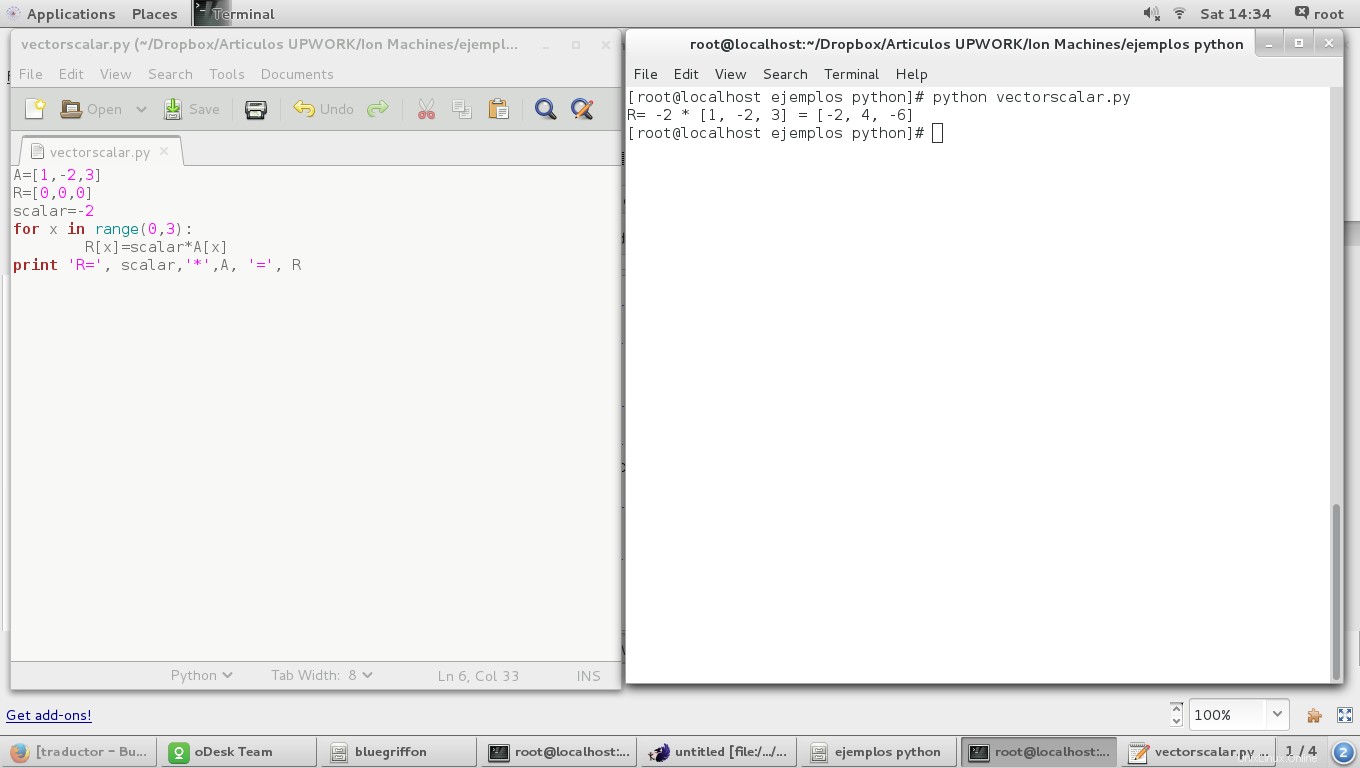
A=[1,-2,3]
e uno scalare:
scalar=-2
prodotto vettore da uno scalare è definito come il prodotto scalare di ciascuna coordinata del vettore:
for x in range(0,3):
R[x]=scalar*A[x]
e il risultato è:
Unit Vector
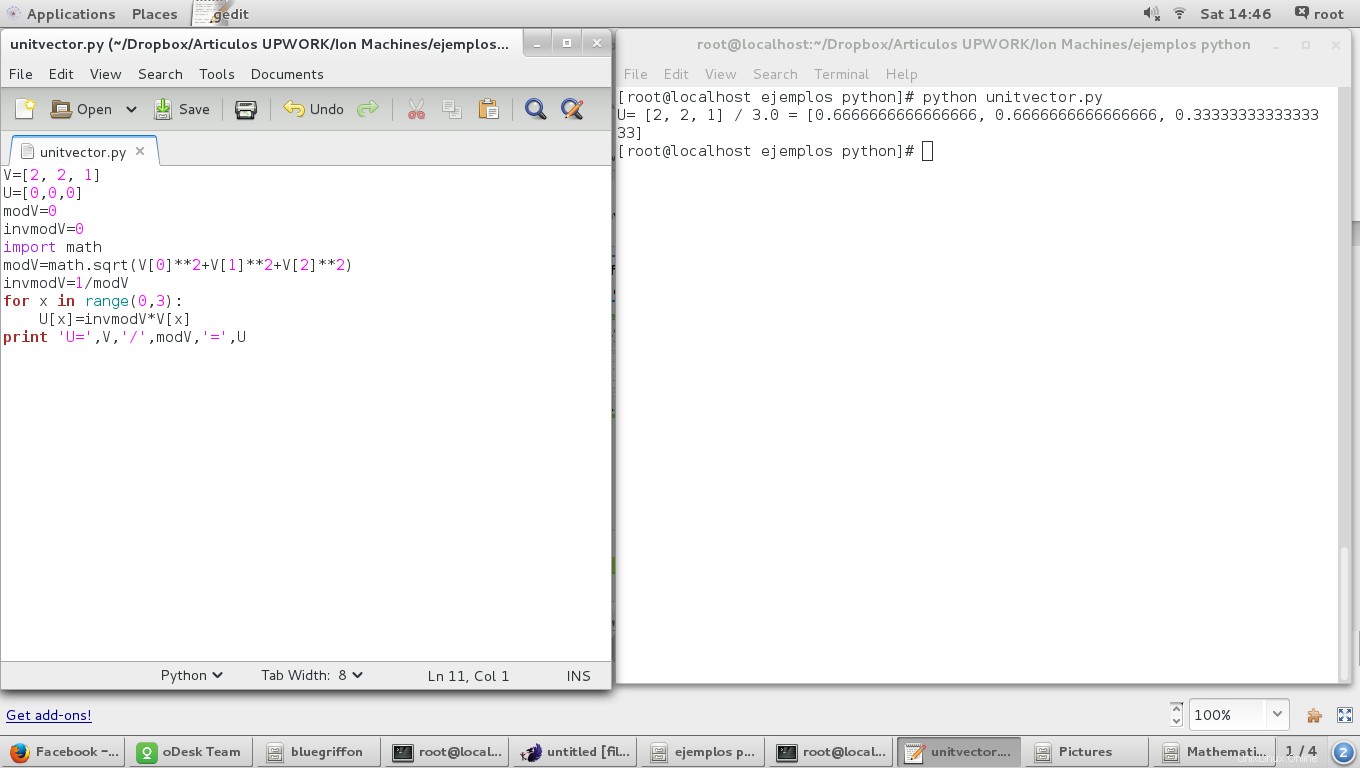
Utilizzando lo script 'Magnitudo di un vettore' abbiamo:
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U
e il risultato è:
Combinazione lineare
Dati tre vettori, A, B e C, possiamo calcolare i valori scalari che, moltiplicati rispettivamente per B e C, risultano nel vettore A. In altre parole, ponendo il vettore A come combinazione lineare dei vettori B e C :
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
Una combinazione lineare porta ad un sistema di equazioni, 3 equazioni con 2 variabili (scalari) se tre vettori r3, oppure 2 equazioni con 2 variabili se sono due vettori in R3, che possono risolversi applicando un determinante di una matrice. Qui dobbiamo fare un punto a causa dei tipi di dati gestiti da Python. In molti casi, quando si calcolano gli scalari coinvolti in una combinazione lineare, il risultato avrà cifre decimali, che si tradurranno in operazioni in virgola mobile. I tipi di dati numerici, gestiti da Python, sono:Integer, Real, Long. Quindi, dobbiamo inserire le coordinate dei vettori come tipo di dati Real, quindi questi rappresentano numeri reali (virgola mobile). Dobbiamo conoscere e comprendere alcune caratteristiche del tipo di dati in Python:
- Intero occupa meno spazio di memoria rispetto al tipo Reale.
- Le operazioni con Real sono più lente di Integer.
Qui abbiamo gli stessi vettori, ma dichiarati come tipo Real:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
Quindi, con questo possiamo scambiare i vettori e quindi avere sempre la soluzione del sistema.
Il primo controllo che dobbiamo fare è se c'è o meno complanarità tra i vettori, quindi sapere se c'è o meno è una combinazione lineare. Per questo, implementeremo una matrice determinante:
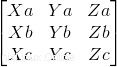
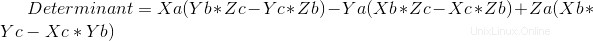
Codice:
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
Se questo determinante è uguale a zero (0) allora c'è una dipendenza lineare tra i vettori e possiamo continuare a calcolare gli scalari. Come accennato in precedenza, il sistema di equazioni ha tre equazioni con due variabili, ottenendo un sistema compatibile determinato, per il quale dobbiamo prendere due delle tre equazioni e risolvere valori scalari, quindi verificare con la terza equazione, non presa prima, se la precedente i valori scalari lo risolvono. Se non lo risolvono, allora non c'è una Combinazione Lineare.
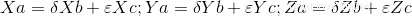
Qui abbiamo il codice completo:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
E il risultato:
[[email protected] ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[[email protected] ejemplos python]#
In conclusione, l'algebra vettoriale di base risulta in una serie di operazioni che coinvolgono sistemi lineari di equazioni e/o semplici operazioni aritmetiche con numeri reali. In un altro tutorial vedremo come possiamo sviluppare prodotti con vettori, come prodotto punto, prodotto incrociato o prodotto misto.