Nel tutorial precedente, abbiamo visto i semplici passaggi per leggere, scrivere e riprodurre file audio. Abbiamo anche visto come possiamo sintetizzare un file audio da una funzione periodica come la funzione coseno. In questo tutorial, vedremo come possiamo apportare aggiunte ai segnali, moltiplicando i segnali (modulazione) e applicando alcune funzioni matematiche di base per vedere il loro effetto sul segnale originale.
Aggiunta di segnali
La somma di due segnali S1(t) e S2(t) dà come risultato un segnale R(t) il cui valore in ogni istante è la somma dei valori di segnale aggiunti in quel momento. Proprio così:
R(t) =S1(t) + S2(t)
Ricreeremo la somma di due segnali in Octave e vedremo l'effetto graficamente. Per prima cosa genereremo due segnali di frequenze diverse per vedere il segnale risultante dalla somma.
Fase 1:creazione di due segnali di frequenze diverse (file ogg)
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs); %writing the function cos(w) on the files created
>> audiowrite(sig2,cos(w2),fs);
Qui tracciamo entrambi i segnali.
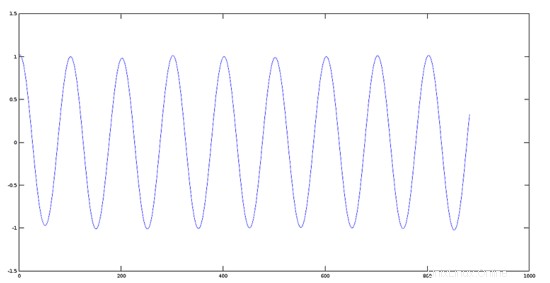
Traccia del segnale 1 (440 Hz)
>> [y1, fs] = audioread(sig1);
>> plot(y1)
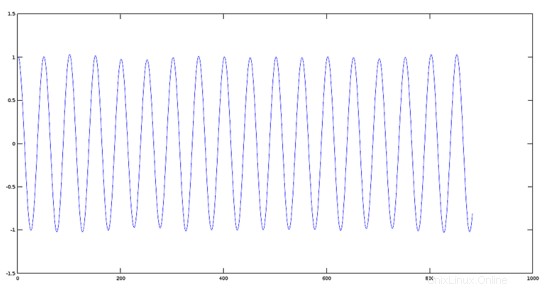
Traccia del segnale 2 (880 Hz)
>> [y2, fs] = audioread(sig2);
>> plot(y2)
Passaggio 2:aggiunta di due segnali
Ora eseguiamo la somma dei due segnali creati nel passaggio precedente.
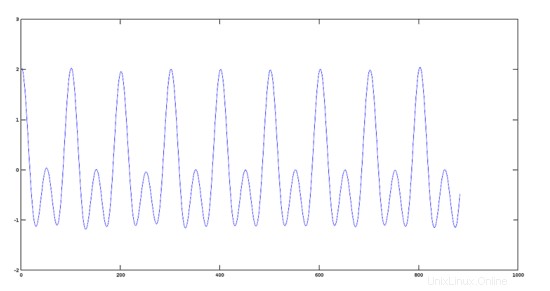
>> sumres=y1+y2;
>> plot(sumres)
Grafico del segnale risultante
L'effetto Octaver
Nell'Octaver, il suono fornito da questo effetto è caratteristico perché emula la nota suonata dal musicista, sia in un'ottava inferiore o superiore (a seconda che sia stata programmata), accoppiata al suono la nota originale, cioè compaiono due note suono identico.
Fase 3:aggiunta di due segnali reali (esempio con due tracce musicali)
A tale scopo utilizzeremo due tracce di canti gregoriani (campionamento vocale).
Pista Avemaria
Per prima cosa leggerò e tramerò una traccia Avemaria:
>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)
Traccia dell'inno
Ora leggerà e tramerà una traccia di inni
>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)
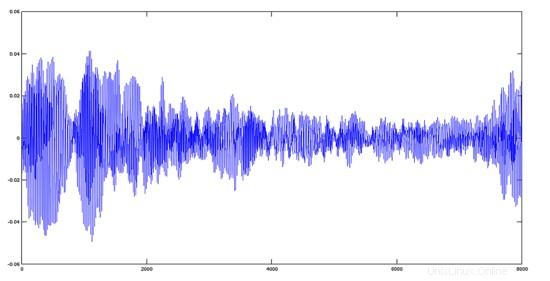
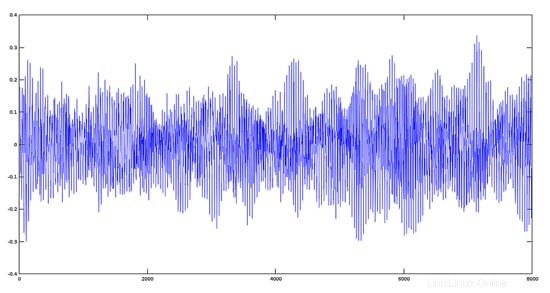
Traccia Avemaria + Hymnus
>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)
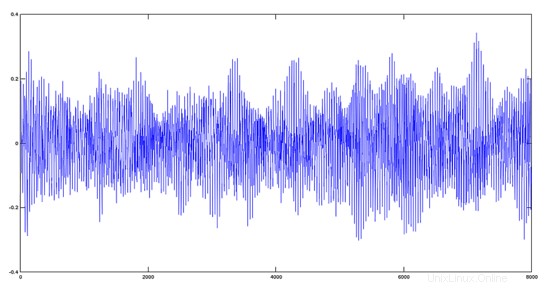
Il risultato, dal punto di vista dell'audio, è che entrambe le tracce suonerà misto.
Prodotto di due segnali
Per moltiplicare due segnali, dobbiamo usare un modo analogo alla somma. Usiamo gli stessi file creati in precedenza.
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> product='prod.ogg'; %creating the audio file for product
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs); %writing the function cos(w) on the files created
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1.*y2, fs); %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod); %plotting the product
Nota:dobbiamo usare l'operando '.*' perché questo prodotto è realizzato, da valore a valore, sui file degli argomenti. Per ulteriori informazioni, fare riferimento al manuale delle operazioni del prodotto con matrici di Octave.
Traccia del segnale prodotto risultante
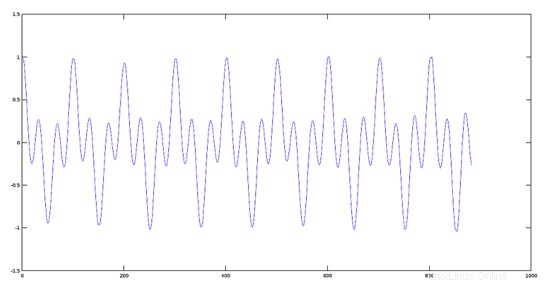
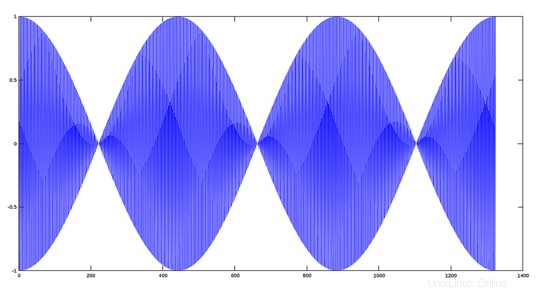
Effetto grafico della moltiplicazione di due segnali con una grande differenza di frequenza fondamentale (Principi di modulazione)
Passaggio 1:
Crea un segnale di frequenza audio con una frequenza di 220 Hz.
>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);
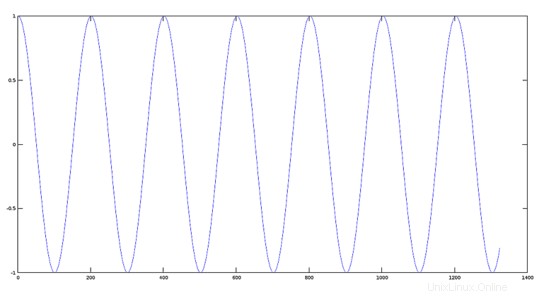
Passaggio 2:
Crea un segnale modulante a frequenza più alta di 22000 Hz.
>> y2=cos(100*w);
>> plot(y2);
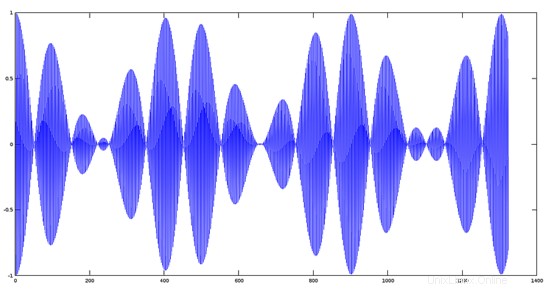
Passaggio 3:
Moltiplicando e tracciando i due segnali.
>> plot(y1.*y2);
Moltiplicare un segnale per uno scalare
L'effetto della moltiplicazione di una funzione per uno scalare equivale a modificarne l'ambito e, in alcuni casi, il segno della fase. Dato uno scalare K, il prodotto di una funzione F(t) per lo scalare è definito come:
R(t) =K*F(t)>> [y,fs]=audioread('cos440.ogg'); %creating the work files
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
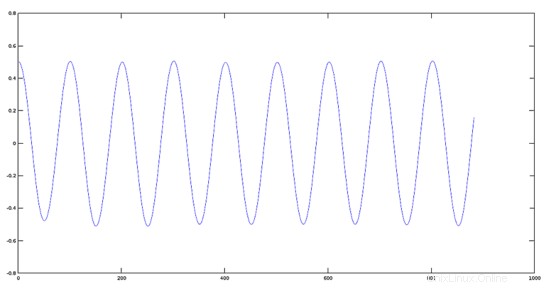
>> K1=0.2; %values of the scalars
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs); %product function-scalar
>> audiowrite(res2, K2*y, fs);
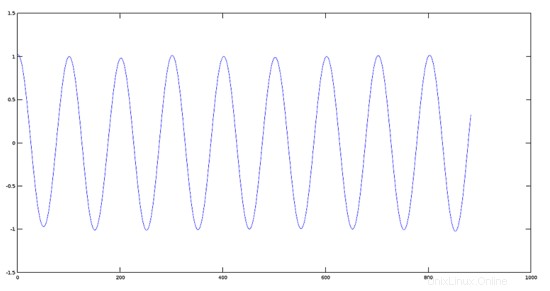
>> audiowrite(res3, K3*y, fs); Trama del segnale originale
>> plot(y)
Traccia di un segnale ridotto in ampiezza di 0,2
>> plot(res1)
Traccia di un segnale ridotto in ampiezza di 0,5
>> plot(res2)

Traccia di un segnale con fase invertita
>> plot(res3)
Conclusione
Le operazioni matematiche di base, come la somma algebrica, il prodotto e il prodotto di una funzione per uno scalare sono la spina dorsale di operazioni più avanzate tra cui l'analisi dello spettro, la modulazione in ampiezza, la modulazione angolare, ecc. Nel prossimo tutorial, vedremo come effettuare tali operazioni e i loro effetti sui segnali audio.